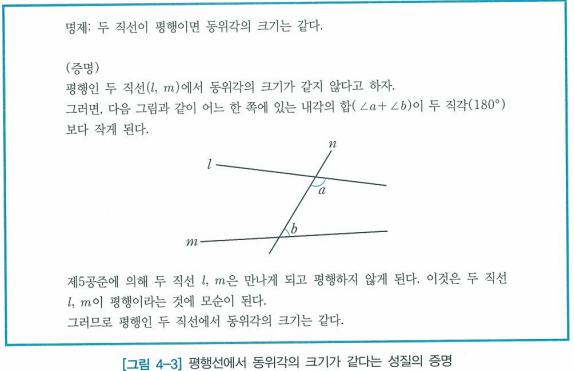
뜻보다 예시 + 문제점을 알아두어야 합니다. 1. 가장 전형적인 종합법의 예시 - 유클리드 제5공준(평행선 공준)을 사용하여 '평행인 두 직선에서 동위각의 크기가 같음'을 증명함. (그니까 모든 증명은, 공준, 공리, 정의에 근거해서 가정으로부터 결론을 이끌어내는 방식으로 이루어짐) cf) 공리, 공준에는 이런 것들이 예시로 있음 2. 분석법 VS 종합법 예시 대부분 분석법을 통해 발견한 증명방법을 거꾸로 되밟아 종합법의 과정을 거쳐 증명을 완성함. 다음 예시를 보면 이해가 잘 됨. 분석법을 통해 결론으로부터 시작하여 선행조건들을 찾아 가정과 연결시키고, 종합법을 통해 가정으로부터 결론을 이끌어내는 것임! 3. 종합적 방식으로만 지도했을 때 문제점 원론처럼 종합적 방식으로만 증명을 기술하면, 어떻게 해서..