이어서 행공간, 열공간, 해공간에 대해 공부하겠습니다.
*행(row), 열(column) 입니다.
18. row space, column space, null space

19. null space
기본행연산은 null space를 바꾸지 않습니다.
기본열연산도 null space를 바꾸지 않습니다.
20. 열공간의 기저 찾는법 (finding basis for a column space)

위 정리를 이해한다면 정말 쉽게 찾을 수 있습니다. 행렬이 REF인 상태에서 leading 1이 있는 열을 찾아주면 됩니다.
만약 REF가 아니라면 기본행연산을 통해 REF로 만들어준 후(이 때 행교환은 하면 안됩니다.) leading 1이 있는 열을 찾아서 원래 행렬에서 고르면 됩니다. 알기 쉽게 예시로 정리 해두겠습니다.

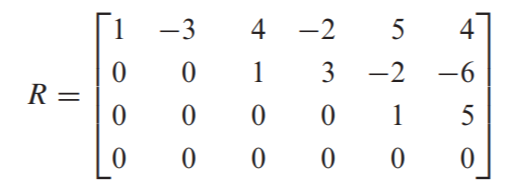

21. 행공간의 기저 찾는 법
열공간의 기저를 찾는 방법과 동일하나 먼저 트랜스포즈 시켜 준 후, 열공간의 기저를 찾아냅니다.
그리고 나서 다시 트랜스포즈 시켜줍니다.

22. Rank(랭크), Nullity
행공간과 열공간은 REF에서와 같은 차원을 가집니다.
랭크는 행공간과 열공간의 공통 기저의 개수(=차원)입니다.

rank = REF일 때 leading 1의 개수
nullity = 자유변수의 개수, 기저의 개수
이렇게 이해하고 있으면 다음이 당연합니다.

랭크는 행렬을 트랜스포즈 해도 같습니다.
23. 직교여공간 (orthogonal complement)

모든 벡터에 대해 직교하는 벡터들을 모아놓은 것을 orthogonal complement 라고 합니다.
property는 다음과 같습니다.

여전히 n차원 실수공간의 부분공간이며, 오직 zero vector만을 공통으로 갖습니다.
또한 직교여공간의 직교여공간은 자기자신입니다.

해공간과 행공간은 직교여공간입니다.
$A$ 의 트랜스포즈 행렬의 해공간과 행렬 $A$의 열공간은 직교여공간입니다.
24. 동치명제들

앞 내용을 모두 이해하고 있으므로 그냥 가볍게 읽고 넘어갑니다.
25. 다음으로 과도결정계와 과소 결정계에 대해 알아보겠습니다.
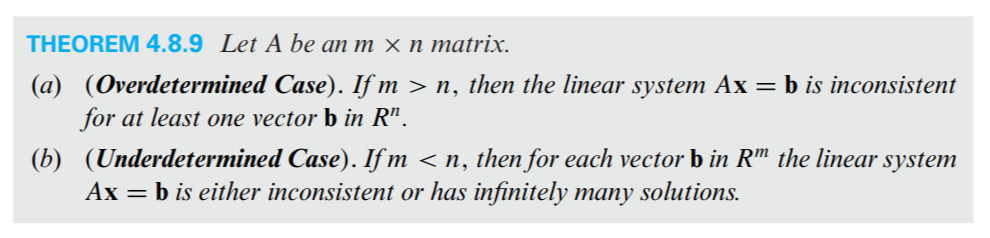
overdetermine된 경우 쉽게 말해 식이 더 많아서 과도결정된 경우를 의미합니다. (세로로 긴 경우)
반대로 underdetermine되면 식보다 미지수가 더 많으므로 자유변수(free variables)가 생기게 되는 것입니다.
(가로로 긴경우)
그래서 무한히 많은 해를 가진다고 표현 하였습니다.
여기까지 정리하고 다음 글에서
26. 고윳값, 고유벡터
부터 이어서 복습하겠습니다.
[reference] Elementary linear algebra - Anton 8,9 edition
'Mathematics > Linear Algebra' 카테고리의 다른 글
| Projection ( + Orthogonal) (0) | 2021.10.27 |
|---|---|
| 선형대수 주요 개념 정리1 (0) | 2021.08.13 |